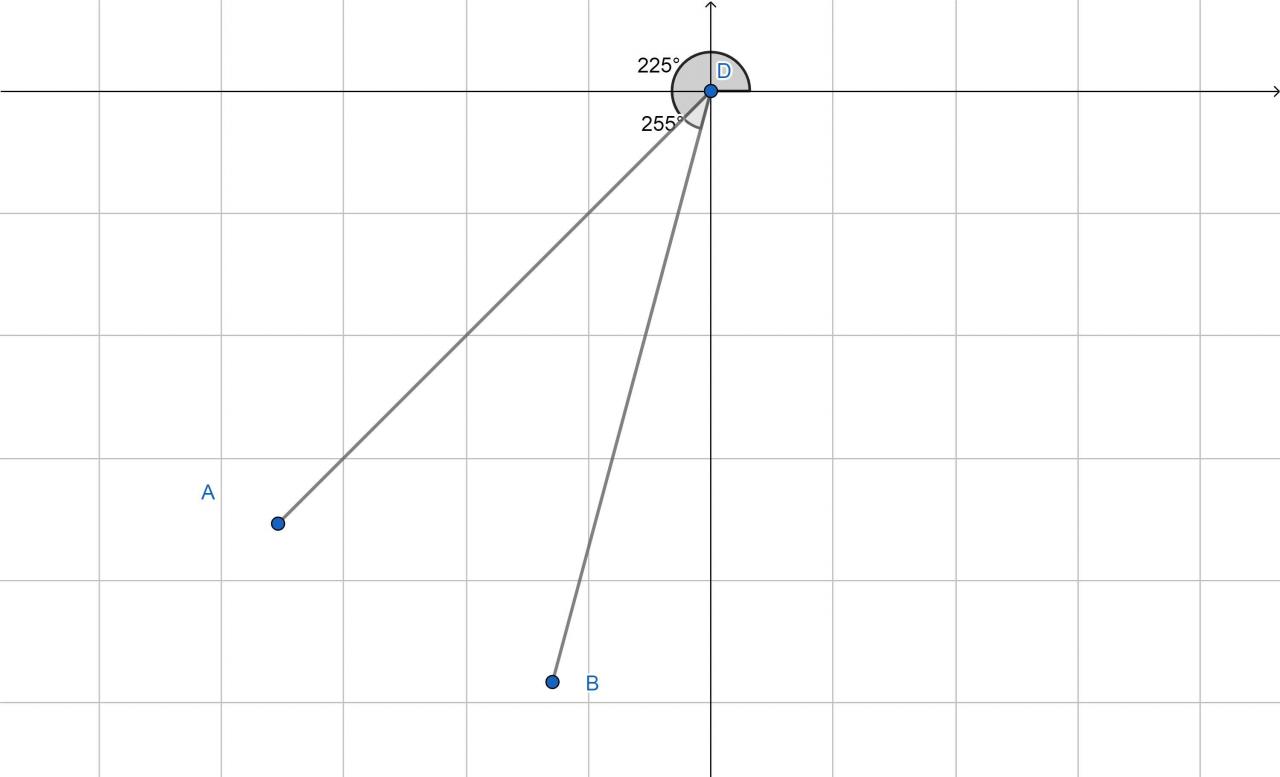
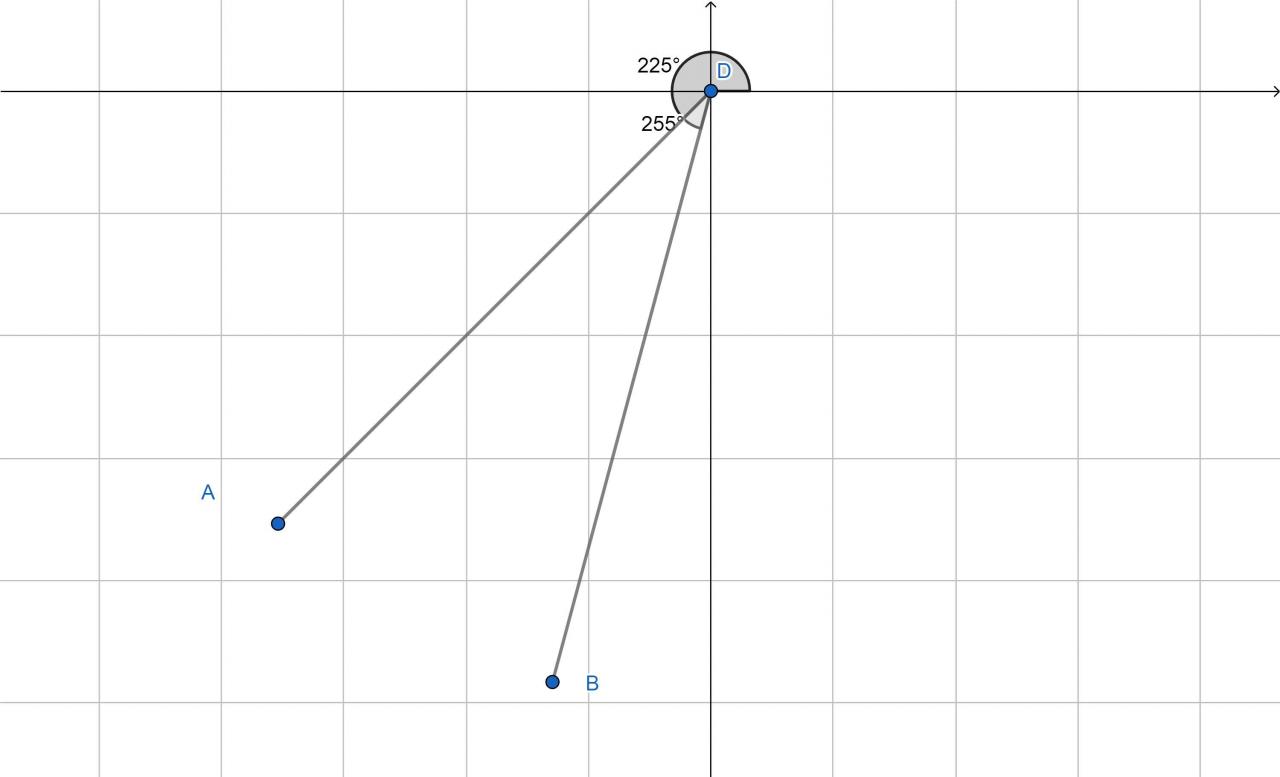
kapal A dan B berada di pelabuhan tanjung pada pukul 09.00 kedua kapal siap berlayar. kapal A menuju arah 225 derajat dengan kecepatan 40 km/jam sedangkan kapal B menuju arah 255 derajat dengan kecepatan 100 akar 3 km/jam. tentukan jarak antara kapal A dan B pada pukul 11.00

kapal A dan B berada di pelabuhan tanjung pada pukul 09.00 kedua kapal siap berlayar. kapal A menuju arah 225 derajat dengan kecepatan 40 km/jam sedangkan kapal B menuju arah 255 derajat dengan kecepatan 100 akar 3 km/jam. tentukan jarak antara kapal A dan B pada pukul 11.00 ​

Mapel Matematika, Jenjang Sekolah Menengah Atas

Kapal A dan B berada di pelabuhan tanjung pada pukul 09.00. Jarak kedua kapal pada jam 11.00 adalah km.

Penjelasan dengan langkah-langkah:

Diketahui:

• Kapal A dan B berangkat pukul 09.00
• Kapal A menuju arah 225 derajat dengan kecepatan 40 km/jam
• Kapal B menuju arah 255 derajat dengan kecepatan 100 akar 3 km/jam

Ditanya:

Jarak antara kapal A dan B pada pukul 11.00

Pembahasan:

Waktu yang ditempuh saat jam 11.00 = 2 jam.

Jarak yang ditempuh kapal A setelah 2 jam:

40 x 2 = 80 km

Jarak yang ditempuh kapal B setelah 2 jam:

km

Berdasarkan keterangan soal, maka besar sudut yang terbentuk antara kapal A dan B adalah

Sehingga jarak antara kapal A dan B adalah

Pelajari lebih lanjut

Materi tentang trigonometri:

#BelajarBersamaBrainly #SPJ1

Pertanyaan Baru di Matematika

---

Untuk membuat 6 loyang kue di butuhkan 3kg terigu . Berapa kg terigu yg di butuhkan jika membuat 3 loyng kue

Matematika, Sekolah Menengah Pertama

« Penyelesaian Soal »

Untuk membuat 6 loyang kue di butuhkan 3kg terigu . Berapa kg terigu yg di butuhkan jika membuat 3 loyang kue?

________________

Kesimpulan

• Maka, Terigu yang dibutuhkan = 1,5 kg

Semoga Bisa Bermanfaat-!

---

Misalkan a, b, c bilangan real positif yang memenuhi a + b + c = 1. Nilai minimum dari
adalah ……​

Matematika, Sekolah Menengah Atas

misalkan

a + b = x

a + b + c = 1 → x + c = 1

berlaku ketidaksamaan

AM ≥ GM

(x + c)/2 ≥ √xc

1/2 ≥ √xc

1/4 ≥ xc

tanda persamaan saat x = c,

maka didapat x = c = √1/4 = 1/2

x = a + b

a + b = 1/2

AM ≥ GM

(a + b)/2 ≥ √ab

1/4 ≥ √ab

1/16 ≥ ab

a = b, maka a = b = √1/16 = 1/4

nilai min

(a + b)/(abc)

= (1/4 + 1/4)/(1/4 . 1/4 . 1/2)

= (1/2)/(1/32)

= 32/2

= 16

a + b + c = 1

---

1 1/3 × 7 4/5 – 0.90 + 75% =…..

tolong kak, beserta caranya​

Matematika, Sekolah Dasar

Jadi, hasilnya adalah 10,25 atau atau

.

Pecahan adalah suatu bilangan yang umumnya terdiri dari dua bilangan. Pecahan dinyatakan dalam bentuk . A dalam bilangan tersebut berperan sebagai pembilang, dan B dalam bilangan tersebut berperan sebagai penyebut. Pecahan artinya membagi antara pembilang dengan penyebutnya. Terdapat 6 macam pecahan, penjelasannya ada di bawah ini.

1. Pecahan biasa

Pecahan biasa terdiri atas dua bilangan yaitu pembilang dan penyebut. Angka yang berada di atas disebut pembilang dan angka yang berada di bawah disebut penyebut. Pecahan biasa terbagi menjadi dua, yaitu pecahan biasa murni, dan pecahan biasa tidak murni. Pecahan biasa murni adalah bilangan pecahan yang pembilangnya lebih kecil daripada penyebutnya. Pecahan biasa tidak murni adalah bilangan pecahan yang pembilangnya lebih besar daripada penyebutnya, sehingga dapat dijadikan pecahan campuran.

2. Pecahan campuran

Pecahan campuran adalah bilangan pecahan yang terdiri atas tiga bilangan yaitu bilangan cacah/bilangan positif, pembilang, dan penyebut. Cara mengubah pecahan campuran menjadi pecahan biasa yaitu dengan mengkalikan penyebut dengan bilangan cacahnya, kemudian dijumlahkan dengan pembilang.

3. Pecahan desimal

Pecahan desimal adalah pecahan yang umumnya bernominal “koma” di belakang suatu bilangan yang bermakna perseratus, perseribu, dan sebagainya. Pecahan desimal berbeda dengan jenis-jenis pecahan yang lainnya. Contohnya: 1,25 ; 205, 5 ; 75,675, dll.

4. Pecahan persen

Pecahan persen adalah bilangan pecahan yang diikuti dengan simbol “%” yang mempunyai makna bilangan tersebut dibagi 100. Karena, persen artinya adalah “perseratus”. Contoh: 75%, 100%, 50%, dll.

5. Pecahan permil

Pecahan permil hampir sama dengan pecahan persen. Hanya saja, bedanya persen artinya “perseratus”, namun permil artinya “perseribu”. Pecahan permil adalah bilangan pecahan yang diikuti dengan simbol “‰” maknanya bilangan tersebut dibagi 1000.

6. Pecahan senilai dan tidak senilai

Pecahan senilai artinya bilangan penyebut dengan pembilang mempunyai nilai yang sama, atau masih bisa disederhanakan lagi dengan angka yang sama. Contohnya: masih bisa disederhanakan lagi dengan membaginya pakai angka 2 menjadi . Sedangkan pecahan tidka senilai adalah pecahan yang pembilang dan penyebutnya memiliki nilai yang tidak sama alias sudah tidak bisa disederhanakan lagi.

.

– 0,90 + 75% = …?

JAWAB:

– 0,90 + 75%

– 0,90 + 75%

Kita ubah ke bentuk desimal

= 10,4 – 0,90 + 0,75

= 9,5 + 0,75

= 10,25

Jadi, hasilnya adalah 10,25 atau atau

.

1. Contoh soal pecahan beserta dengan langkah penyelesainnya:
2. Jenis-jenis pecahan:
3. Soal tentang pecahan senilai:

.

Kelas: IV

Mapel: Matematika

Bab: 6 – Pecahan

Kode kategorisasi: 4.2.6

Kata kunci: Menyelesaikan soal pecahan

Pecahan adalah bilangan yang dapat disajikan dalam bentuk a/b, dengan a, b bilangan bulat dan b # 0. Dalam hal ini, a disebut sebagai pembilang dan b disebut sebagai penyebut.

• Pecahan biasa, yaitu pecahan yang pembilangnya lebih kecil dari penyebutnya.

Contoh :               

• Pecahan campuran, yaitu pecahan yang ditulis sebagai jumlah dari bilangan cacah dan pecahan biasa.

Contoh :

• Pecahan desimal, yaitu bilangan yang

terdiri atas dua angka atau lebih dan

disertai tanda koma yang memiliki arti

persepuluhan, perseratusan, perseribuan

dan sebagainya.

Contoh : 0,2; 0,14; 2,6; 10,07 dst

• Pecahan persen, yaitu bilangan

pecahan yang penyebutnya 100.

Pecahan persen dilambangkan dengan

tanda ( % ) yang artinya per 100.

Contoh :

• Pecahan permil, yaitu bilangan pecahan

yang penyebutnya 1.000. Pecahan permil

dilambangkan dengan tanda ( % ).

Contoh :

a. Operasi penjumlahan pecahan

Operasi penjumlahan pecahan dapat dilakukan bilamana penyebutnya sama. Jika penyebutnya berbeda, harus disamakan terlebih dahulu dengan mencari KPK (Kelipatan Persekutuan Kecil) dari penyebut penyebutnya.

Contoh :

Contoh :Berpenyebut sama :

Berpenyebut tidak sama :

b. Operasi pengurangan pecahan

Operasi pengurangan pecahan juga dapat dilakukan bilamana penyebutnya sama. Jika penyebutnya berbeda, harus disamakan terlebih dahulu dengan mencari KPK (Kelipatan Persekutuan Kecil) dari penyebut penyebutnya.

Contoh :

Contoh :Berpenyebut sama :

Berpenyebut tidak sama :

c. Operasi perkalian pecahan

Operasi perkalian pecahan dilakukan dengan cara mengalikan pembilang dengan pembilang dan penyebut dengan penyebut. Berbeda dengan operasi penjumlahan pecahan dan pengurangan, operasi perkalian pecahan dapat dilakukan tanpa mencari KPK (Kelipatan Persekutuan Kecil) dari penyebut pecahan.

Contoh :

d. Operasi pembagian pecahan

Operasi pembagian pecahan dilakukan dengan cara mengalikan pecahan yang dibagi dengan kebalikan dari pecahan pembagi. Dalam hal ini, kebalikan dari suatu pecahan, yaitu pembilang dan penyebut pada pecahan tersebut ditukar letaknya sehingga pembilang menjadi penyebut dan penyebut menjadi pembilang.

Contoh :

Suatu pecahan dapat diubah menjdi bentuk pecahan yang lain. Misalnya, pecahan biasa dapat diubah menjadi persen atau pecahan desimal diubah menjadi pecahan biasa.

Cara mengubah suatu pecahan menjadi bentuk pecahan yang lain dapat dilakukan dengan memperhatikan sifat sifat jenis pecahan tersebut.

Penyelesaian soal:

» JAWABAN BY : RACHELLNGAB «

#CMIIW

=> DETAIL JAWABAN : <=

– Mapel : Matematika

– Kelas : 5 SD (Sekolah Dasar)

– Materi : Bab 5 – Pecahan

– Kode Soal : 2

– Kode Kategorisasi : 5.2.5

---

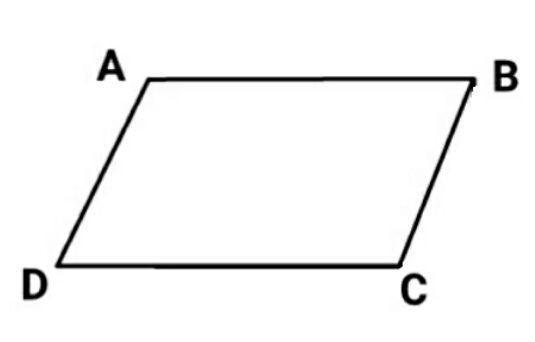
Umumnya pada suatu jajargenjang berlaku …. A. sudut-sudutnya sama besar
B. mempunyai sumbu simetri
C diagonal-diagonalnya sama panjang
D. mempunyai dua pasang sisi yang sejajar

Matematika, Sekolah Dasar

Jawaban:

B.mempunyai sumbuh simetri

Penjelasan dengan langkah-langkah:

maaf kalo salah

Umumnya pada suatu jajar genjang berlaku…

Mempunyai dua pasang sisi yang sejajar (Opsi D). ✔️✔️

Pembahasan ~

Jajar genjang dikenal sebagai bangun datar yang memiliki dua pasang sisi yang sejajar. Yaitu rusuk atas sejajar dengan rusuk bawah, rusuk kiri sejajar dengan rusuk kanan.

Contoh :

Kita coba untuk membuktikan dari jajar genjang yang ada di foto. Disana ada 2 pasang sisi yang sejajar, yaitu :

• AB sejajar dengan DC
• AD sejajar dengan BC

---

Semua toko tersebut menjual barang yang sama Jenis dan harga / Nama Toko dan besar diskon satuan barang. Kemeja: 150.000
Celana: 200.000

Toko Aneka: Kemeja 25% dan Celana 10%
Toko Burza: Kemeja 20% dan Celana 15%
Toko Citra: Kemeja 15% dan Celana 20%
Toko Dewi: Kemeja 10% dan Celana 25%

Syfa ingin membeli sebuah celana dan sebuah baju ditoko yang sama. Agar mendapat harga yang paling murah, di toko mana ia harus berbelanja? Jelaskan!​

Matematika, Sekolah Menengah Pertama

Jadi, yang paling murah ada di toko Dewi