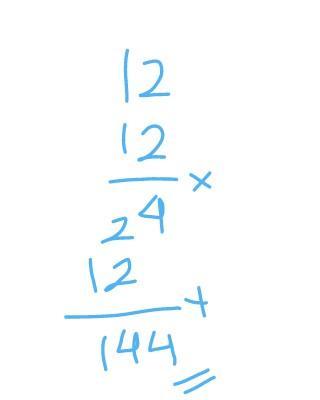
Jika PQ = i + 3j +2k, maka 3PQ adalah2. Diberikantigabuahvektormasing-masing sebagai berikut: p=i+j+k
q=2-3j+k
r = -2j-3k Jika s = 2p – q + 3r, maka s =….
a. i + 2j-7k
b.-i +6k
c. 6i + 7k
d. -j-8k
e.j+4k
Mapel Matematika, Jenjang Sekolah Menengah Atas
Penjelasan dengan langkah-langkah:
2(111)-(2-31) + 3(0-2-3)=(222)+(-23-1)+(0-6-9)=(0-1-8)=-j-8k
Daftar Isi
Pertanyaan Baru di Matematika
Lim x -> 2 (x – 2)/(1 – sqrt(x – 1)) =
Matematika, Sekolah Menengah Atas
limit tak tentu
bentuk 0/0
L’Hopital
turunkan pembilang dan penyebut
lim x→2 (x – 2)/(1 – √(x – 1))
= lim x→2 (x – 2) / (1 – (x – 1)^1/2)
= lim x→2 (1 – 0) / (0 – 1/2 (x – 1)^-1/2)
= lim x→2 – 2√(x – 1)
= -2√(2 – 1)
= -2
Penyelesaian:
Kesimpulan:
Maka, hasilnya adalah –2.
Kuiis. ====================================
Tentukan nilai dari:
=> pakai cara✓
Matematika, Sekolah Menengah Pertama
Jawaban:
Penjelasan dengan langkah-langkah:
Limit
Limit
Pendahuluan
Hellow semuanya^^ , kali ini saya akan berbagi sedikit materi tentang ”Limit” yang biasa dijumpai pas kelas 11 yah. Izinkan saya untuk menerangkannya y^^/. Semoga memahaminya!
Sering kita dengar saat SMA kata limit ini. Dan sering juga kita dengar bahwa limit itu ialah…yup Limit secara singkat berarti mendekati. Sedangkan, Limit pada fungsi ialah limit dengan variabelnya yang mendekati suatu fungsi, baik positif maupun negatif.
Teorema Limit :
==> dengan k adalaha konstanta.
Jika
, maka
, dengan k adalah konstanta.
Jika
, maka
.
Tips menemukan nilai limit :
1.) Dengan substitusi langsung
Kita hanya memasukkan nilai limitnya pada x (variabel) kedalam fungsi limitnya. Apabila menghasilkan 0/0, maka gunakan cara yg lain.
2.) Pemfaktoran
=> memfaktorkan fungsi dalam limit tersebut. Menghilangkan faktor (x – a), dari pembilang dan penyebut. Lalu apabila ada yang sama kita bisa coret dan menyelesaikannya.
3.) Dikalikan dengan bilangan sekawan
=> Apabila terdapat bentuk akar, maka terlebih dahulu dikalikan sekawan agar bentuk akar hilang, kemudian disederhanakan. ingat lagi konsep rumus aljabar kuadrat salah satunya ialah a² – b² = (a + b)(a – b)
4.) L’Hospital
=> Cara ini juga sering digunakan untuk sincostangen. Biasanya kita gunakan ini ketika cara subtisusi langsung gagal (0/0) maka L’Hospital solusinya. Dimana kita hanya menurunkan fungsi limitnya sampai dapat baik pada pembilang maupun penyebutnya.
Pembahasan
Diketahui :
Ditanya :
Hasil dari tersebut…
Jawaban :
Untuk soal seperti ini, kita bisa menggunakan metode SUBSTITUSI LANGSUNG karena hasilnya masih dapat dicari/ditemukan.
Pelajari Lebih Lanjut :
- Contoh soal limit tak hingga (1) :
- Contoh soal limit tak hingga (2) :
- Contoh soal limit yang difaktorkan lalu disubstitusi (1) :
- Contoh soal limit yang difaktorkan lalu disubstitusi (2) :
- Contoh soal limit metode L’hospital :
Detail Jawaban :
Bab : 7
Sub Bab : Bab 7 – Limit
Kelas : 11 SMA
Mapel : Matematika
Kode kategorisasi : 11.2.6
Kata Kunci : Limit.
Sebuah benda yg massanya 2 Kg ditarik oleh anak dengan gaya 30 N dalam arah mendatar. berapakah kecepatan yang di alami benda tersebut
Matematika, Sekolah Menengah Pertama
a = 15 m/s²
Penjelasan dengan langkah-langkah:
F = 30 N
m = 2 kg
a = F/m
= 30/2
= 15 m/s²
Dengan caranya. 12³+ 10 x 5 =
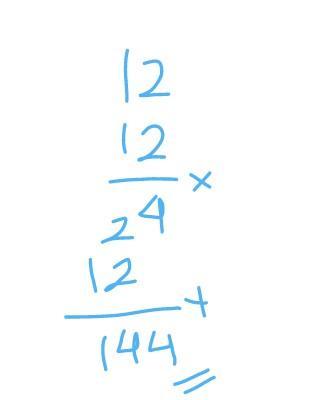
Matematika, Sekolah Dasar
→ 12³ + 10 × 5
= (12 × 12 × 12) + (10 × 5)
= (144 × 12) + 50
= 1.728 + 50
= 1.778
✿✿✿✿✿✿✿✿✿✿✿✿✿✿✿✿✿✿✿✿
Jawaban:
1 .778
Penjelasan dengan langkah-langkah:
- 12³ + 10 × 5
- ( 12 × 12 × 12 ) + 10 × 5
- ( 144 × 12 ) + 10 × 5
- 1.728 + ( 10 × 5 )
- 1.728 + 50
- 1.778
Sebuah balok Memiliki volume 1.200 cm dengan panjang 15cm, dan lebar 10cm maka tinggi tersebut adalah….. Cm 
~
Grade tertinggi = BA (Gpp ga grade)
Menggunakan cara
Matematika, Sekolah Menengah Pertama
✎ t = V : p × l
✎ 1200 : 15 × 10
✎ 1200 : 150
✎ 8 Cm
V = P × L × T
1200 = 15 × 10 × T
1200 = 150 × T
T = 1200/150
T = 8 cm